Sampling Visible GGX Normals
with Spherical Caps
| Jonathan Dupuy | Anis Benyoub |
| Intel Corporation | Intel Corporation |

|

|

|
|

|

|

| GGX VNDF |
|
| spherical caps |
|
linked to
🔗
Contribution
| [Heitz18] |

|
| Ours |

|
|
✓ simpler
|
|
✓ faster
|
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

| GGX VNDF |

|
| spherical caps |

|
linked to
🔗
Contribution
| [Heitz18] |

|
Background
| [Walter et al. 07] |

|
| GGX = "Ground Glass (X)unknown" |


(microsurface)
(equivalent ellipsoid)
Background
| [Walter et al. 07] |

|
| GGX = "Ground Glass (X)unknown" |


(microsurface)
(equivalent ellipsoid)
Background
| [Walter et al. 07] |

|
| GGX = "Ground Glass (X)unknown" |


(microsurface)

(equivalent ellipsoid)
Background
| [Walter et al. 07] |

|
| GGX = "Ground Glass (X)unknown" |


(microsurface)
(equivalent ellipsoid)
Background
| [Walter et al. 07] |

|
| GGX = "Ground Glass (X)unknown" |


(microsurface)

(equivalent ellipsoid)
Background
| [Walter et al. 07] |

|
| GGX = "Ground Glass (X)unknown" |


(microsurface)
(equivalent ellipsoid)
Background
| [Walter et al. 07] |

|
| GGX = "Ground Glass (X)unknown" |


(microsurface)

(equivalent ellipsoid)
Background
| [Walter et al. 07] |

|
| GGX = "Ground Glass (X)unknown" |


(microsurface)
(equivalent ellipsoid)
Background
| [Walter et al. 07] |

|
| GGX = "Ground Glass (X)unknown" |


NDF

(microsurface)
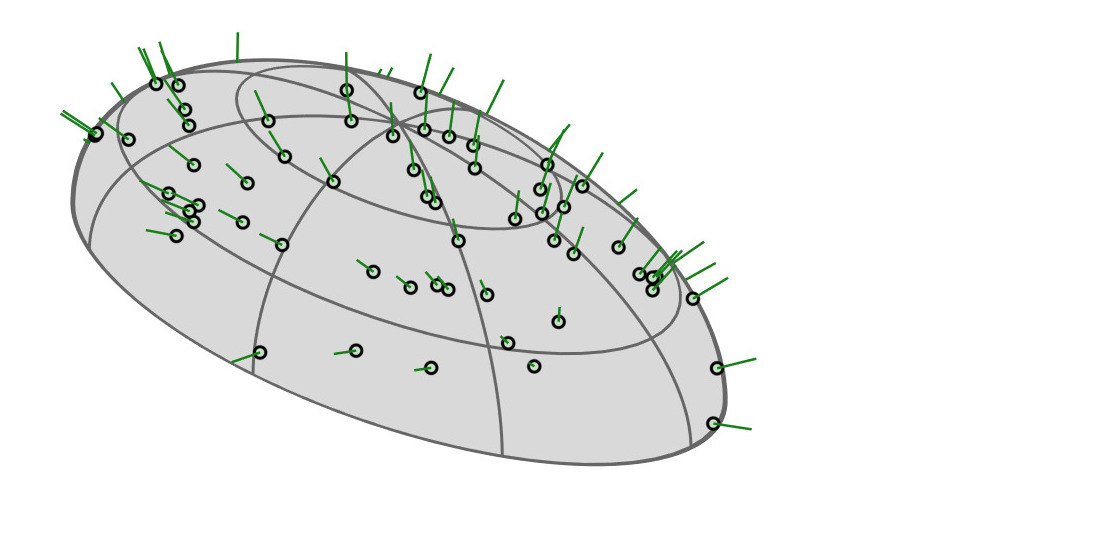
(equivalent ellipsoid)
Background
| [Heitz18] |

|
| GGX VNDF sampler |


VNDF

NDF

incident direction
visible / occluded surface
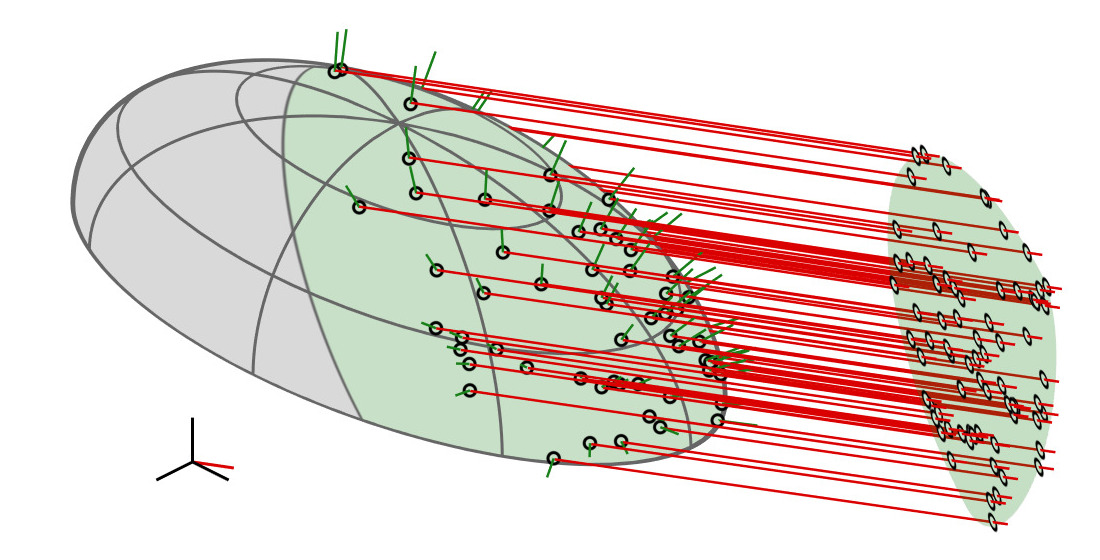
(microsurface)
(equivalent ellipsoid)
visible / occluded surface
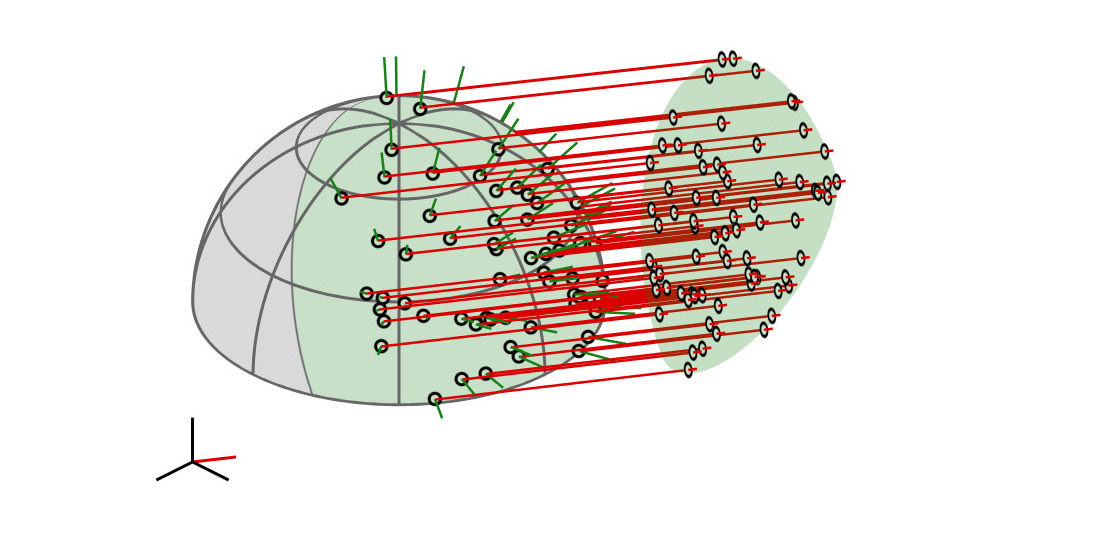




(1) linear transformation

(2) sample
(3) inverse transformation

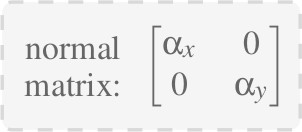
(equivalent ellipsoid)
visible / occluded surface
| GGX sampling code |

|
Background
| [Heitz18] |

|
| GGX VNDF sampler |







(1) linear transformation

(2) sample
(3) inverse transformation

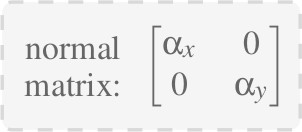
(equivalent ellipsoid)
visible / occluded surface
Background
| GGX sampling code |

|
| [Heitz18] |

|
| GGX VNDF sampler |







(1) linear transformation

(2) sample
(3) inverse transformation

(equivalent ellipsoid)
visible / occluded surface
| hemisphere sampling code |

|
| overview |
| GGX sampling code |

|
Background
| [Heitz18] |

|
| GGX VNDF sampler |
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

| GGX VNDF |

|
| spherical caps |

|
linked to
🔗
| [Heitz18] |

|
Contribution
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

| GGX VNDF |

|
| spherical caps |

|
linked to
🔗
| [Heitz18] |

|
Contribution
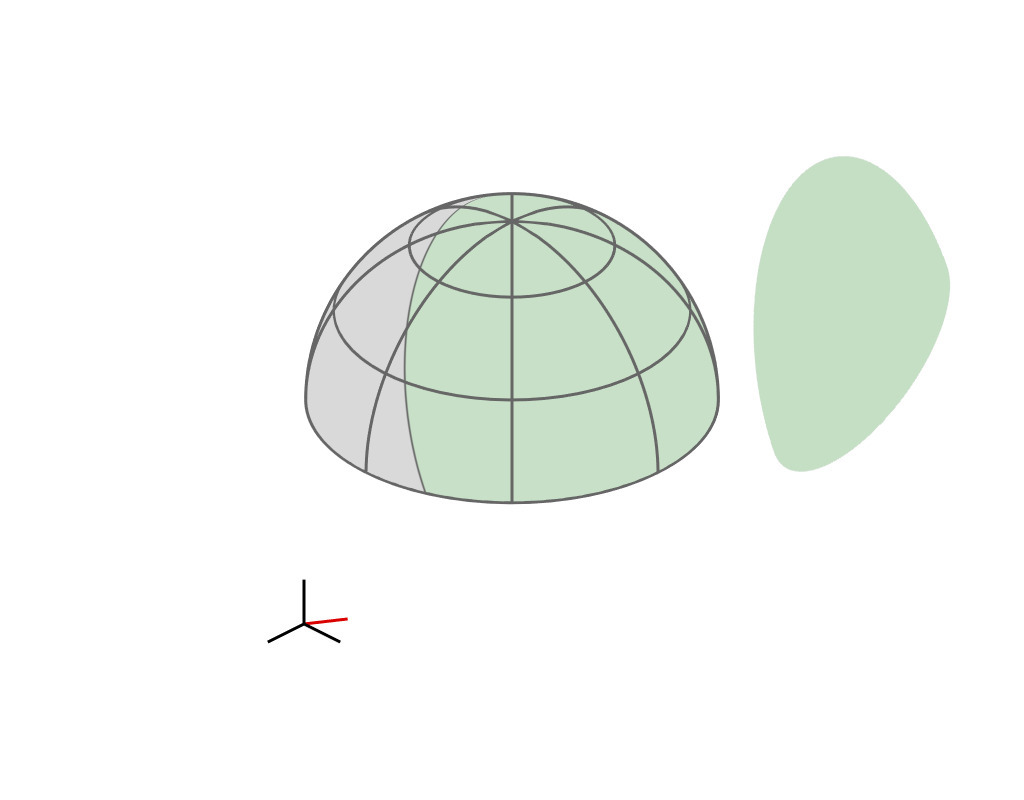
Key Insight
| GGX VNDF | 🔗 | spherical caps |
|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
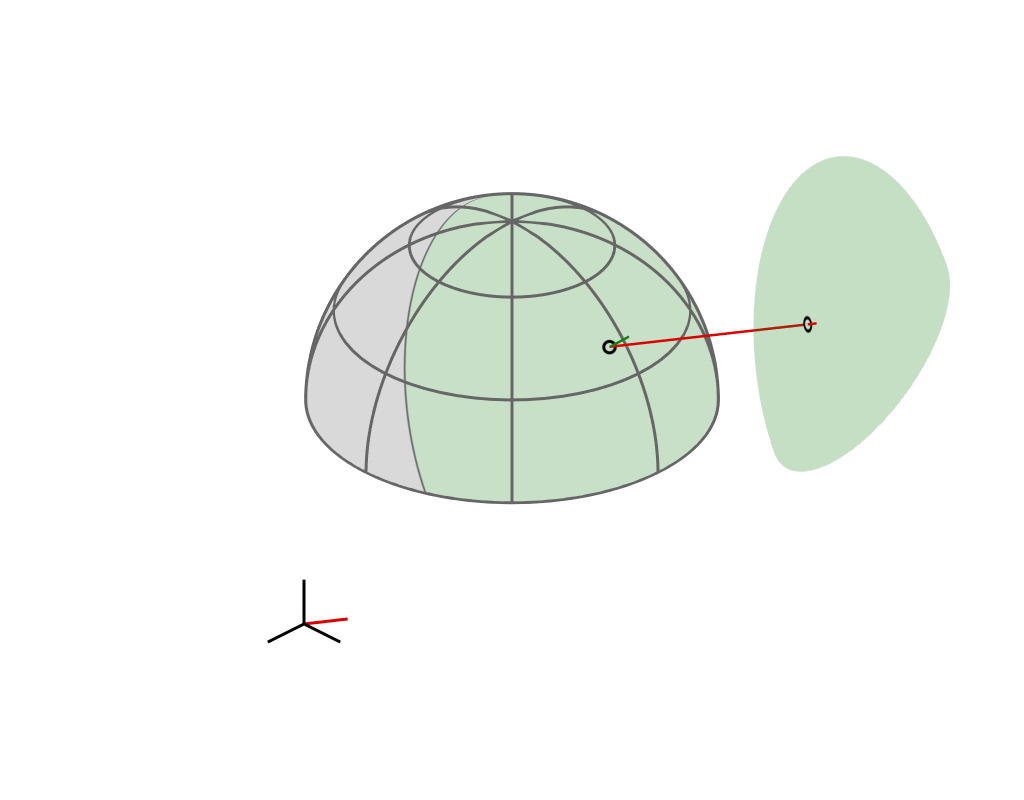
Key Insight
| GGX VNDF | 🔗 | spherical caps |
|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
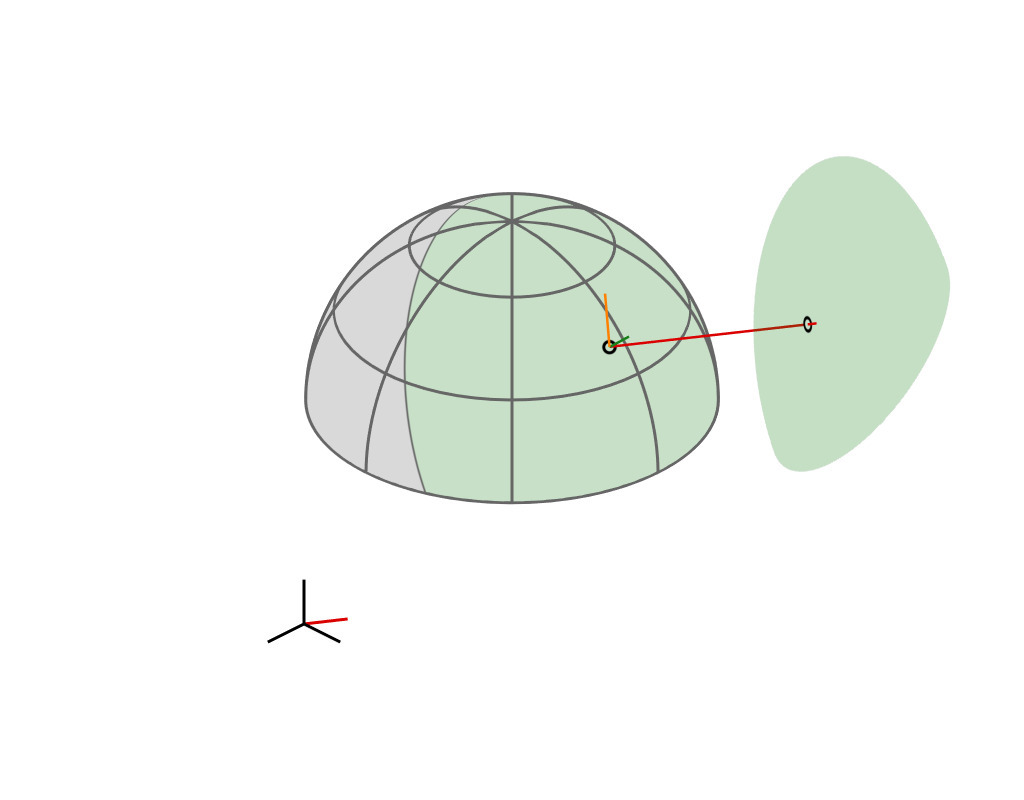
Key Insight
| GGX VNDF | 🔗 | spherical caps |
|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
Key Insight
| GGX VNDF | 🔗 | spherical caps |

|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
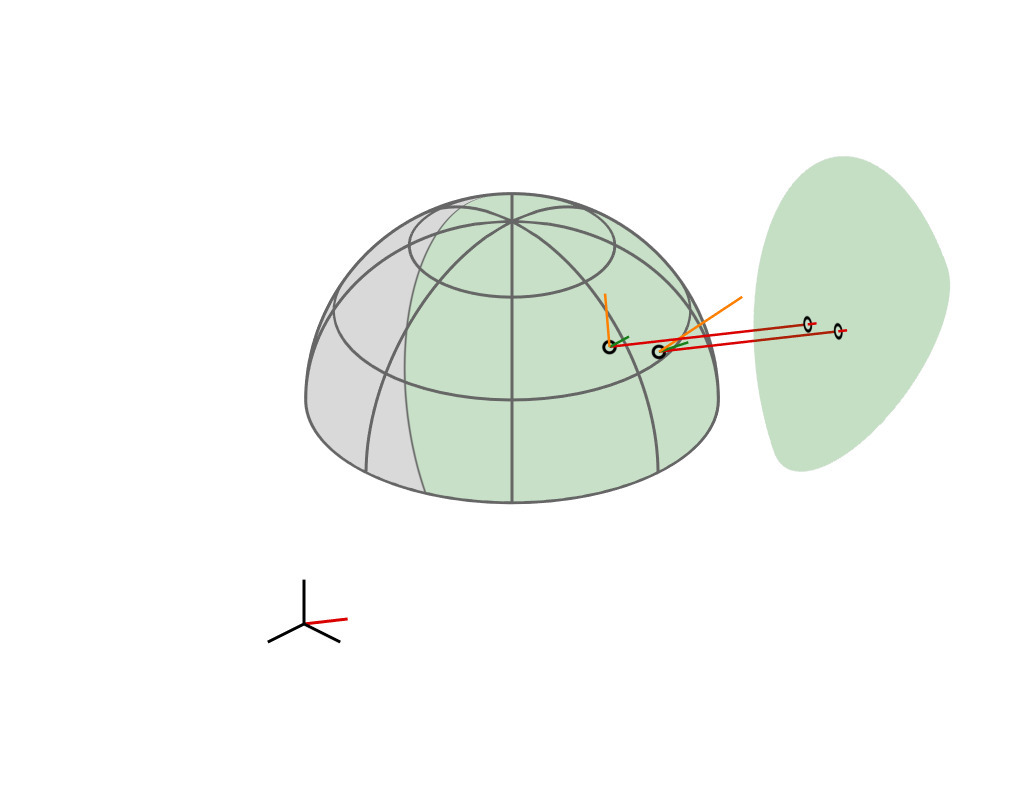
Key Insight
| GGX VNDF | 🔗 | spherical caps |
|
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
Key Insight
| GGX VNDF | 🔗 | spherical caps |
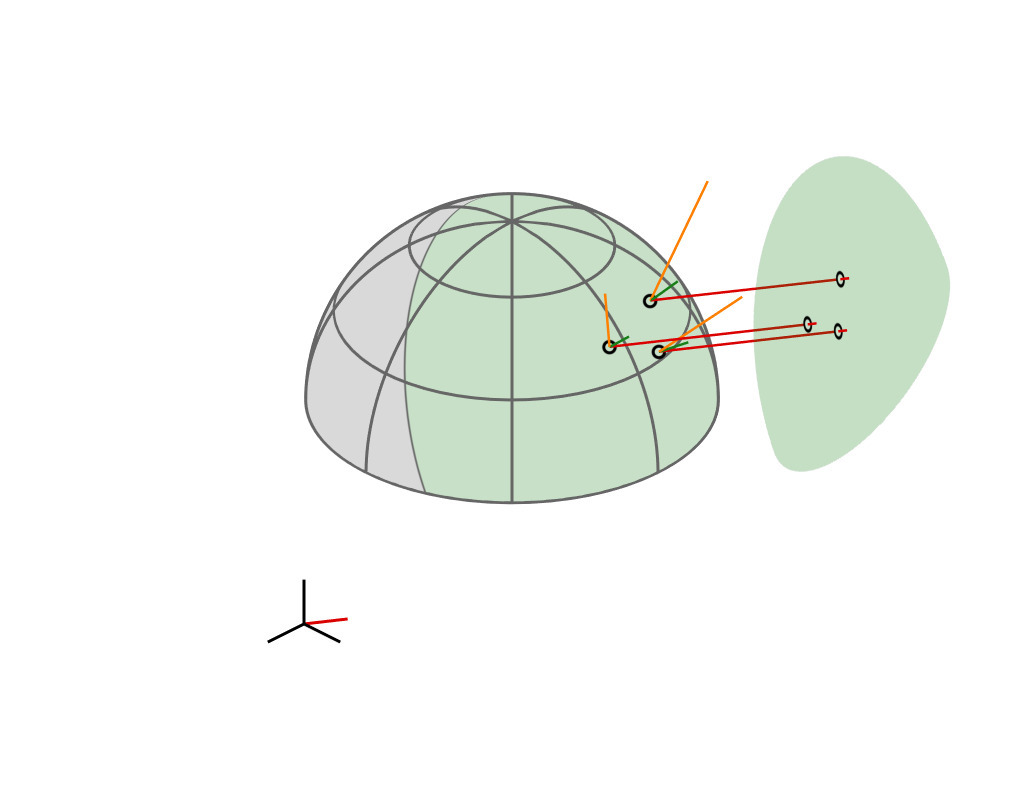
|
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
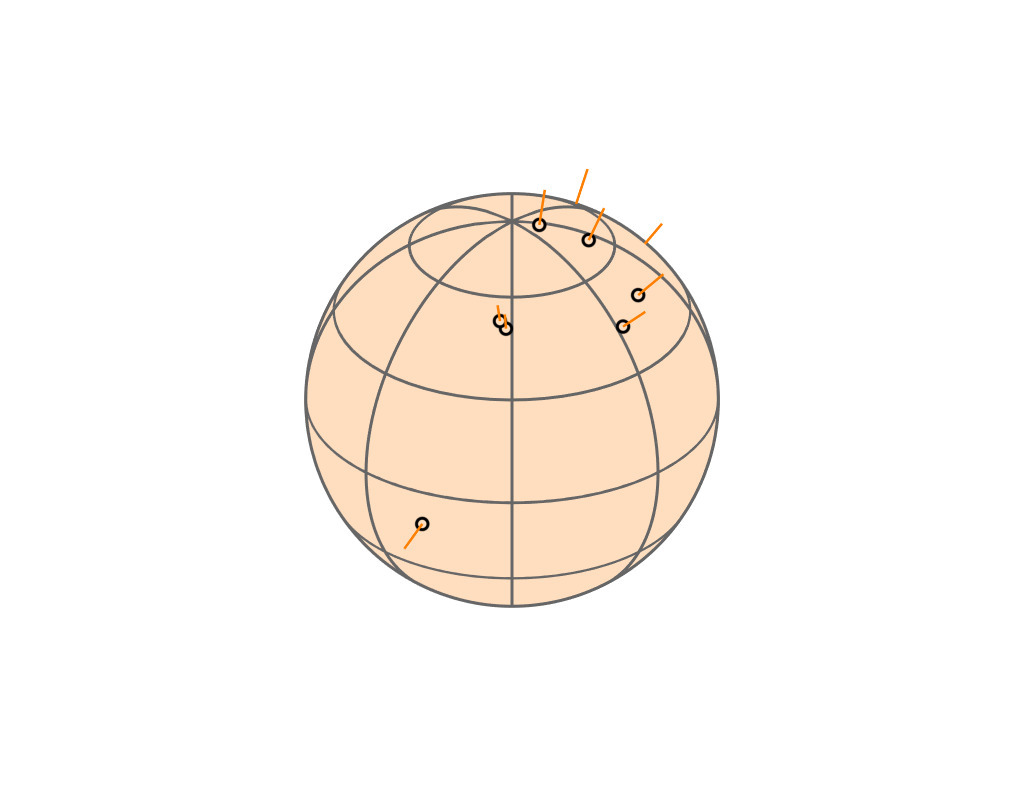
Key Insight
| GGX VNDF | 🔗 | spherical caps |
|
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
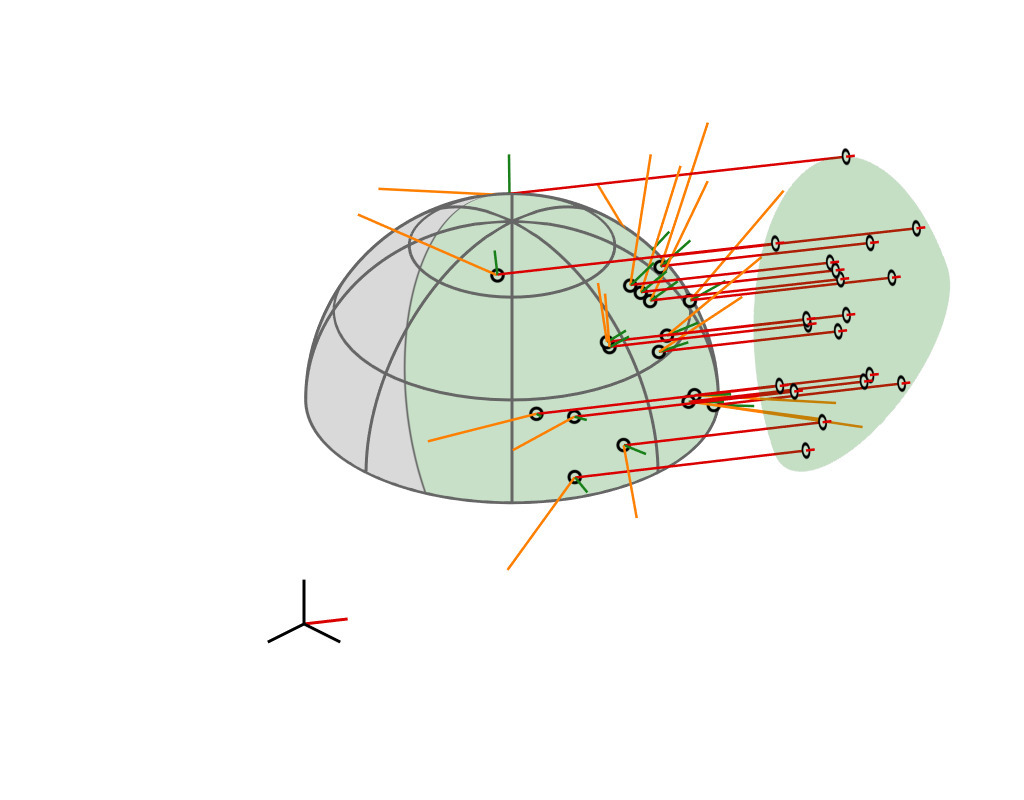
Key Insight
| GGX VNDF | 🔗 | spherical caps |
|
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
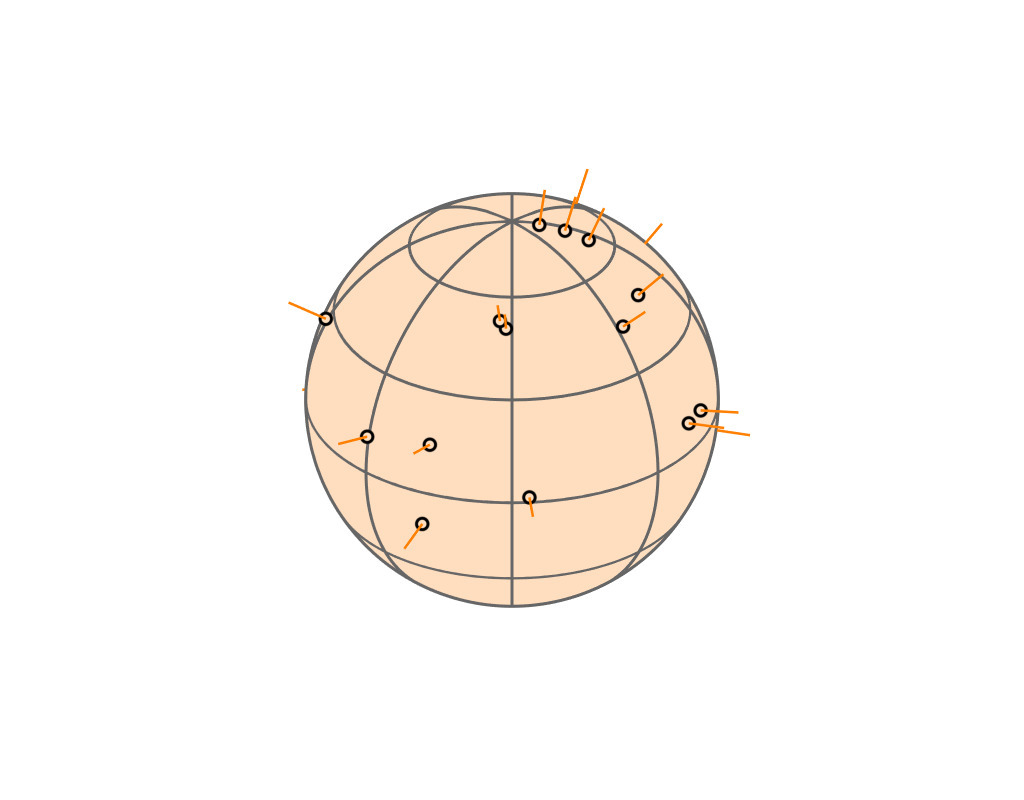
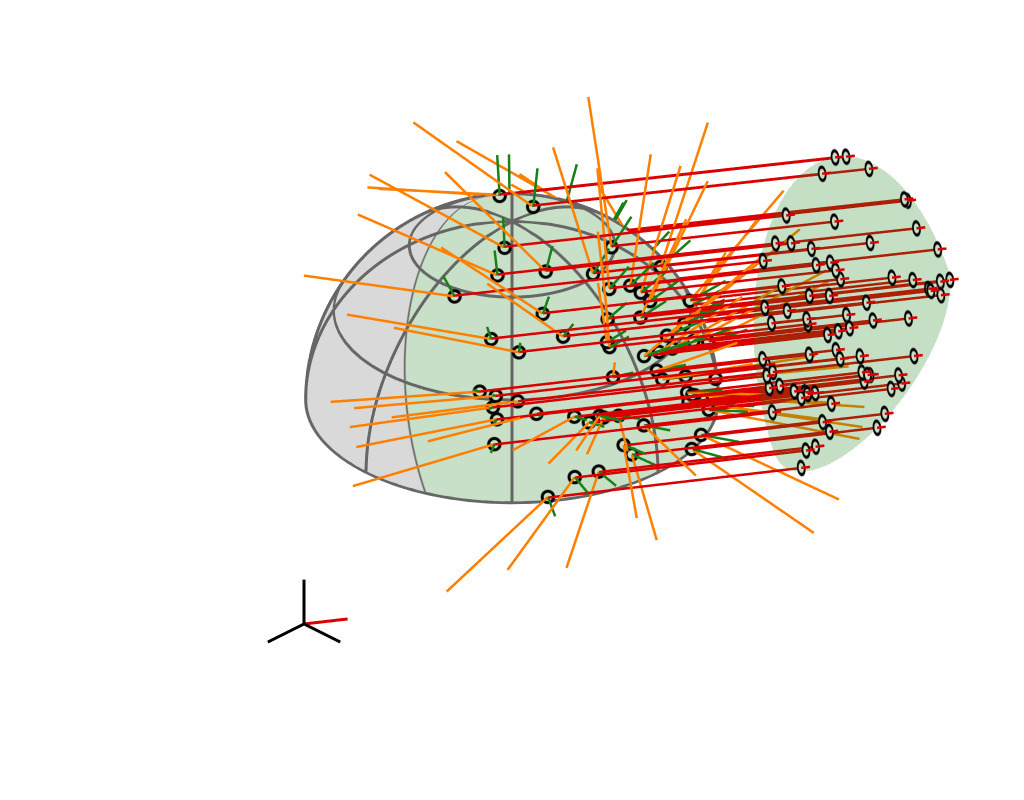
Key Insight
| GGX VNDF | 🔗 | spherical caps |
|
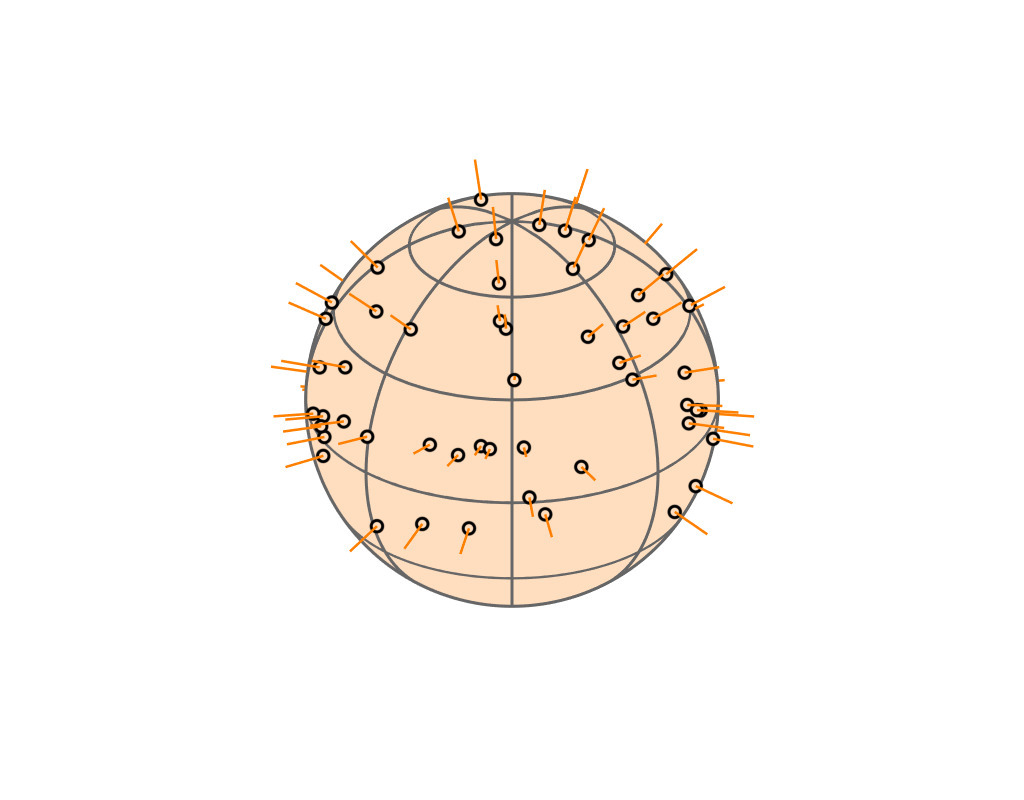
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
Key Insight
| GGX VNDF | 🔗 | spherical caps |
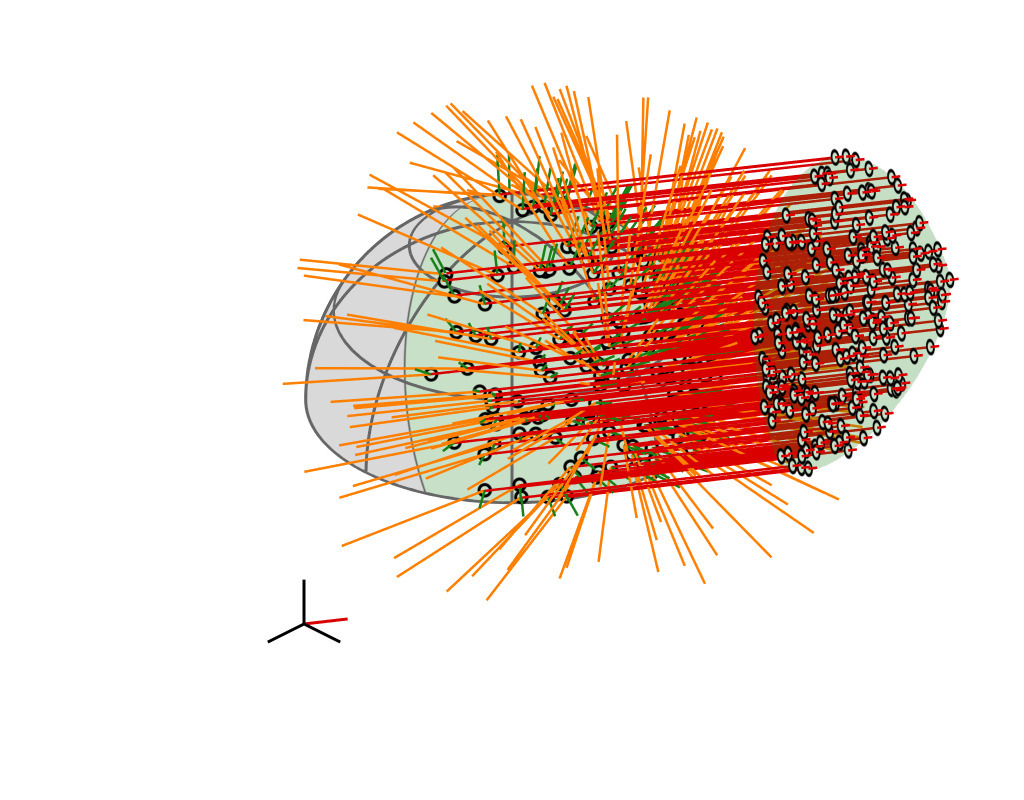
|
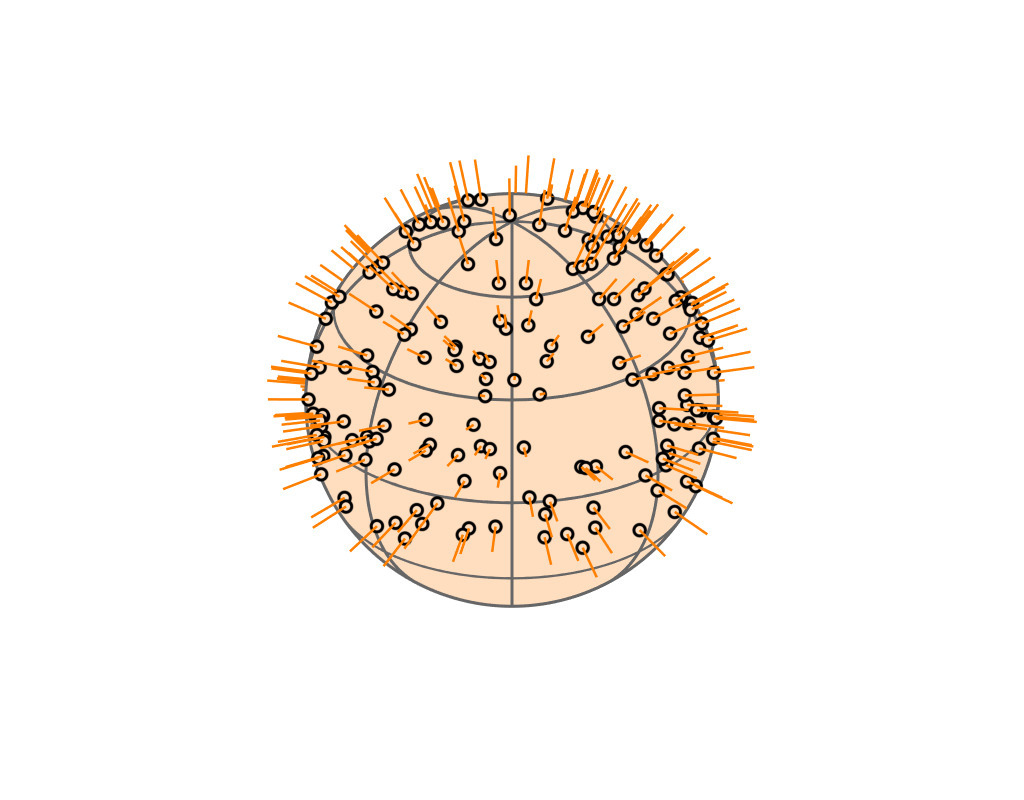
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
Key Insight
| GGX VNDF | 🔗 | spherical caps |

|
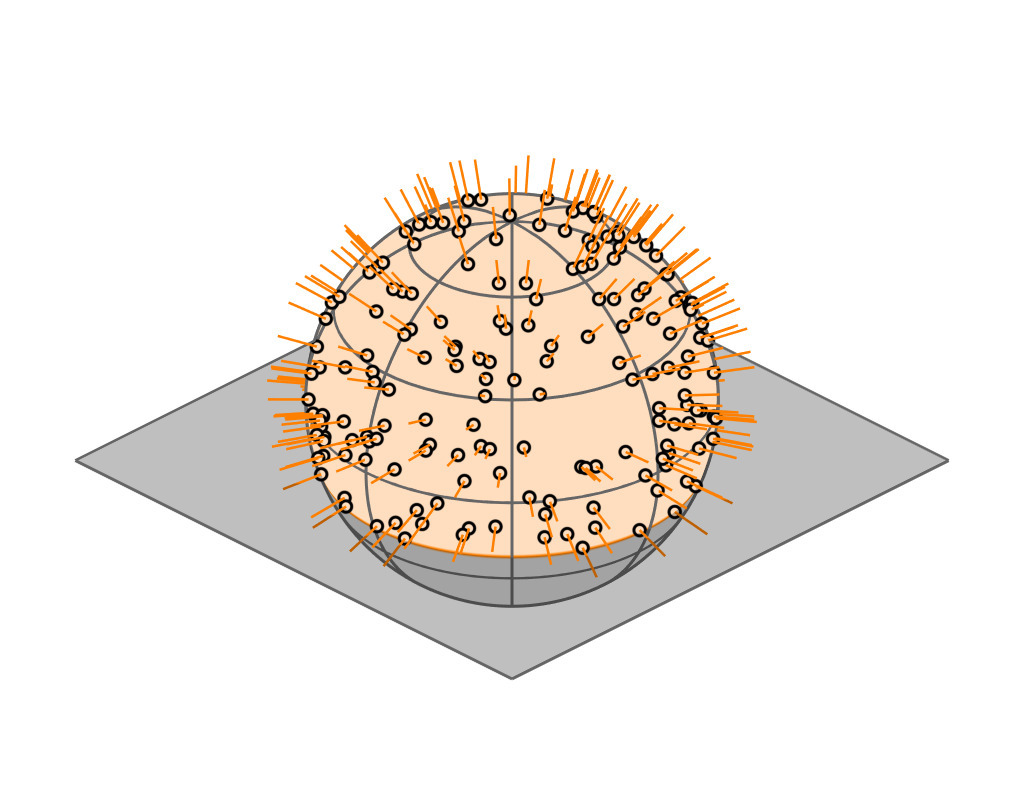
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
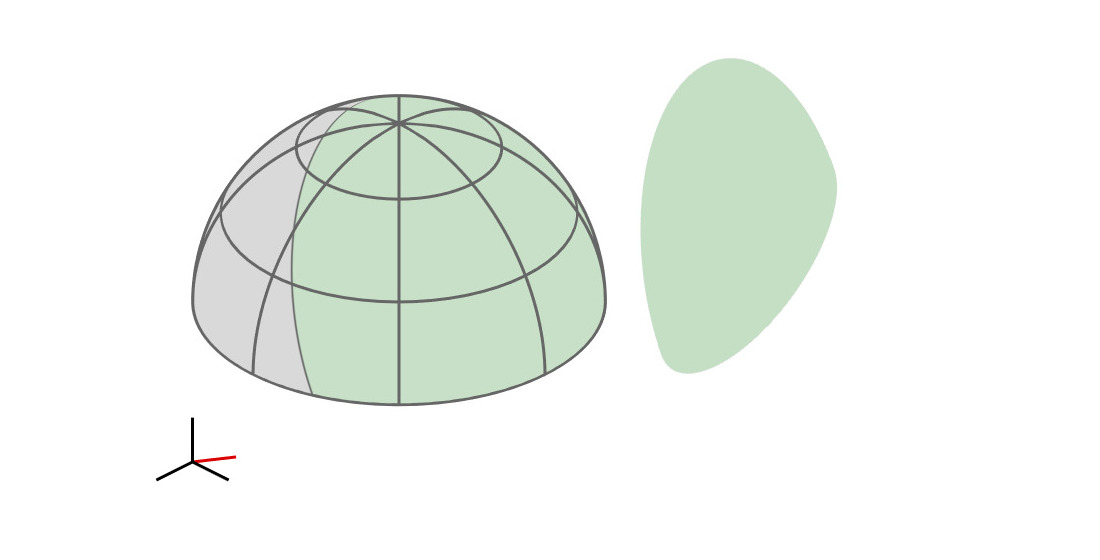
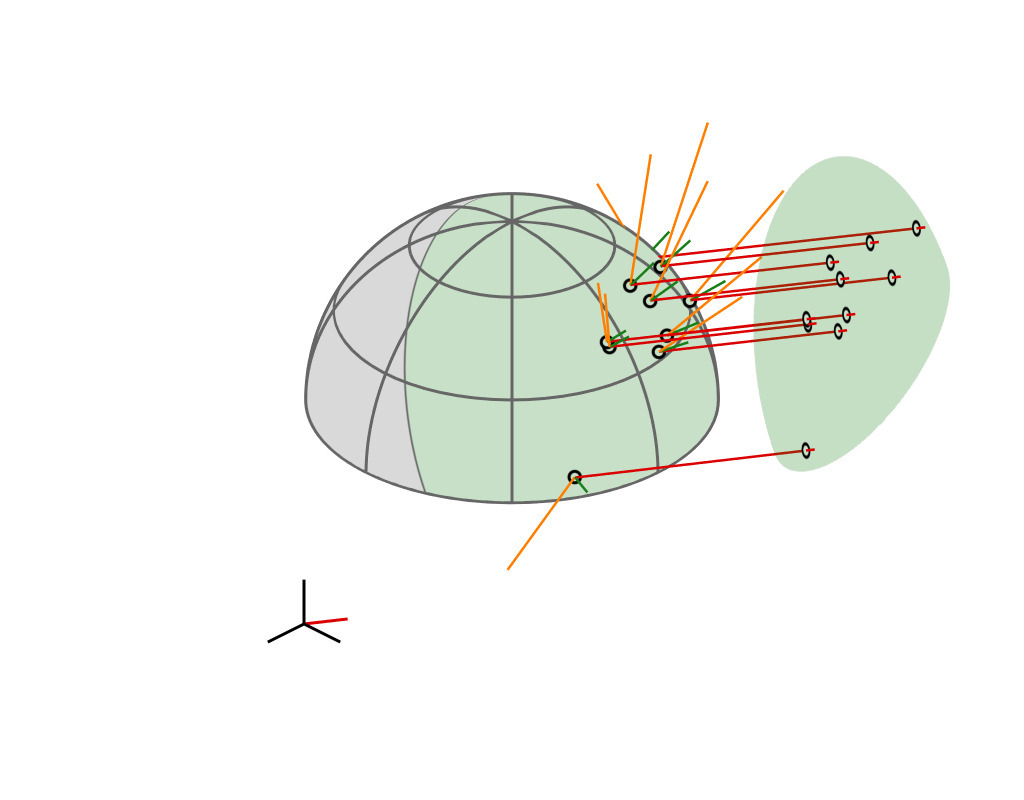
| cutoff plane |
| A hemispherical mirror reflects parallel rays uniformly and within a spherical cap |
(see paper for mathematical proof)
Key Insight
| GGX VNDF | 🔗 | spherical caps |

|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
| A hemispherical mirror reflects parallel rays uniformly and within a spherical cap |
(see paper for mathematical proof)
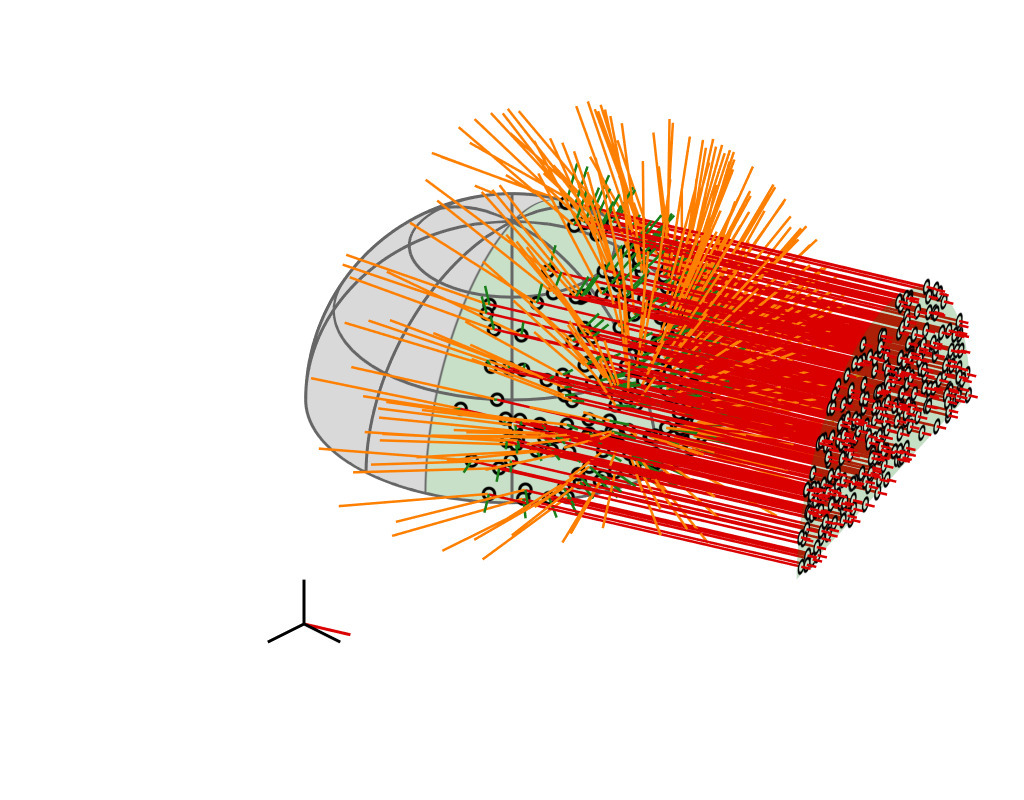
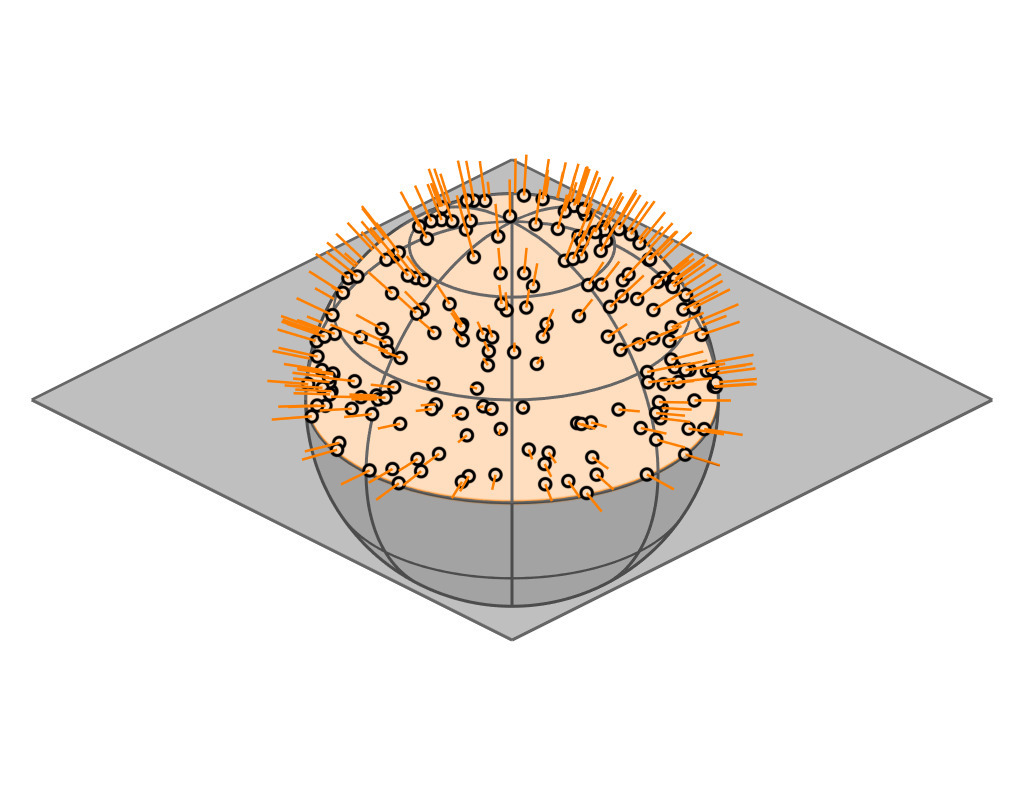
Key Insight
| GGX VNDF | 🔗 | spherical caps |
|
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
| A hemispherical mirror reflects parallel rays uniformly and within a spherical cap |
(see paper for mathematical proof)
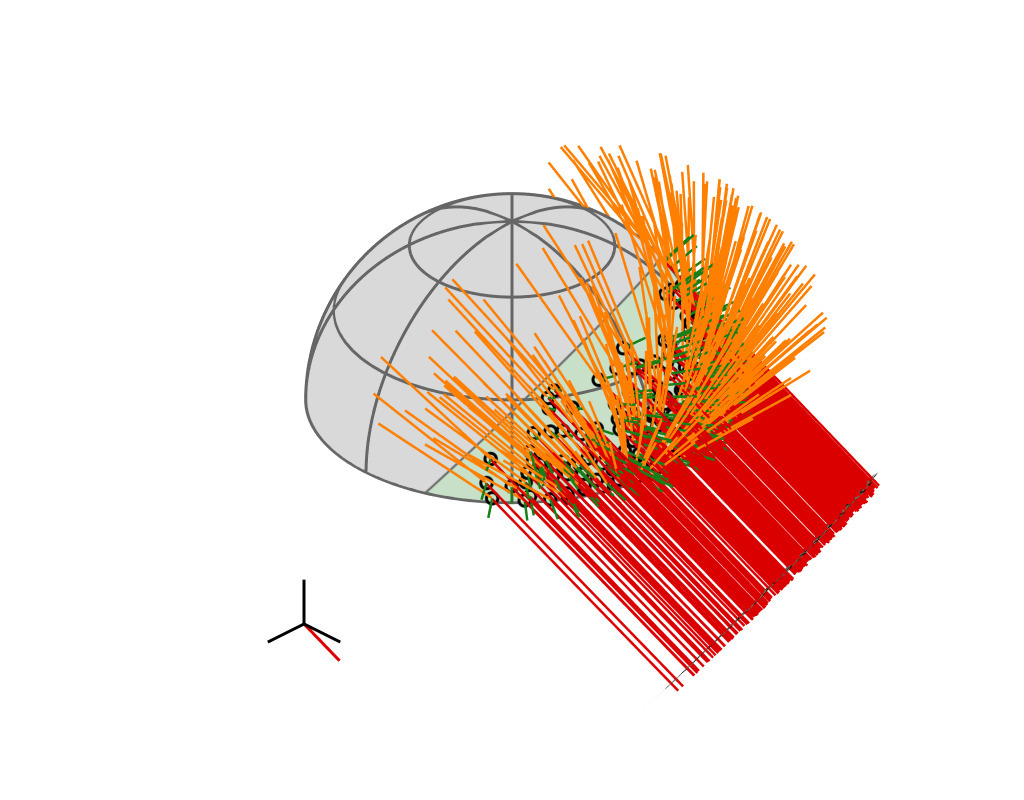
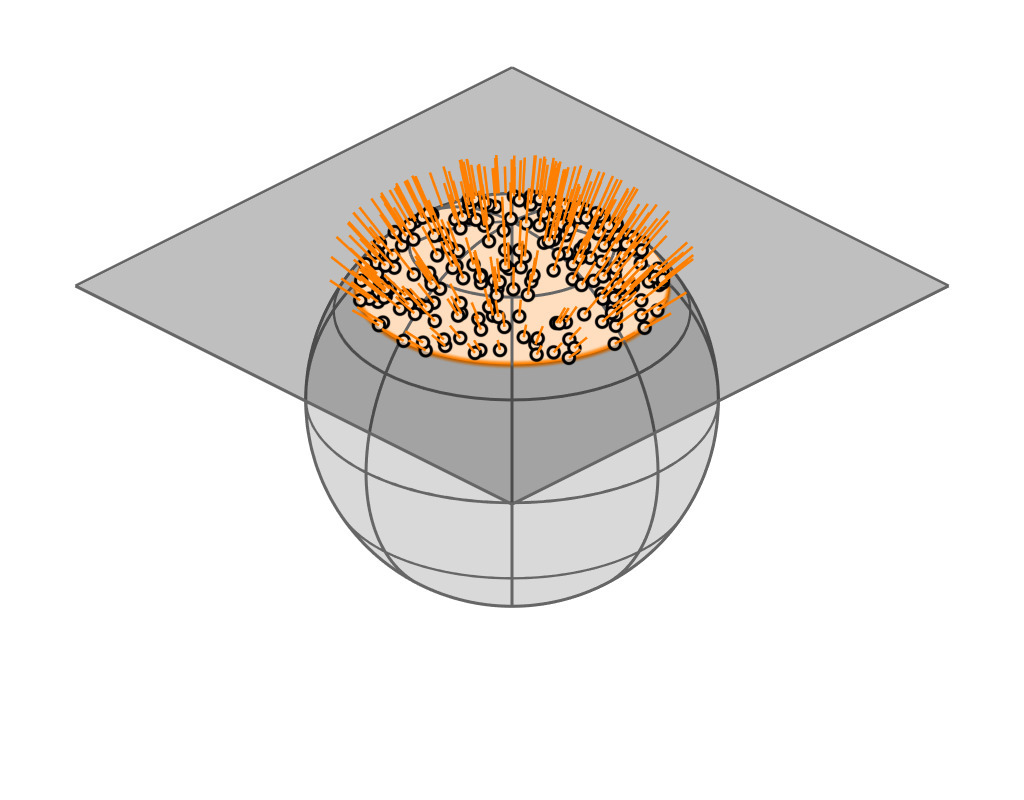
Key Insight
| GGX VNDF | 🔗 | spherical caps |
|
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
| A hemispherical mirror reflects parallel rays uniformly and within a spherical cap |
(see paper for mathematical proof)
Key Insight
| GGX VNDF | 🔗 | spherical caps |
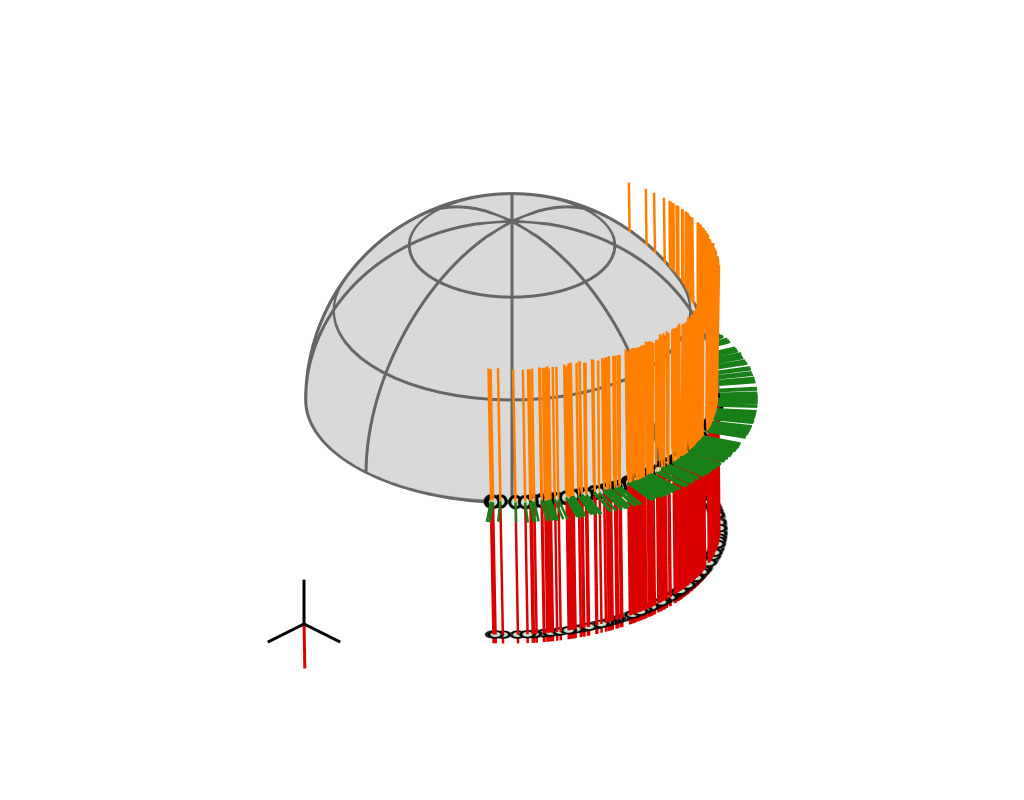
|
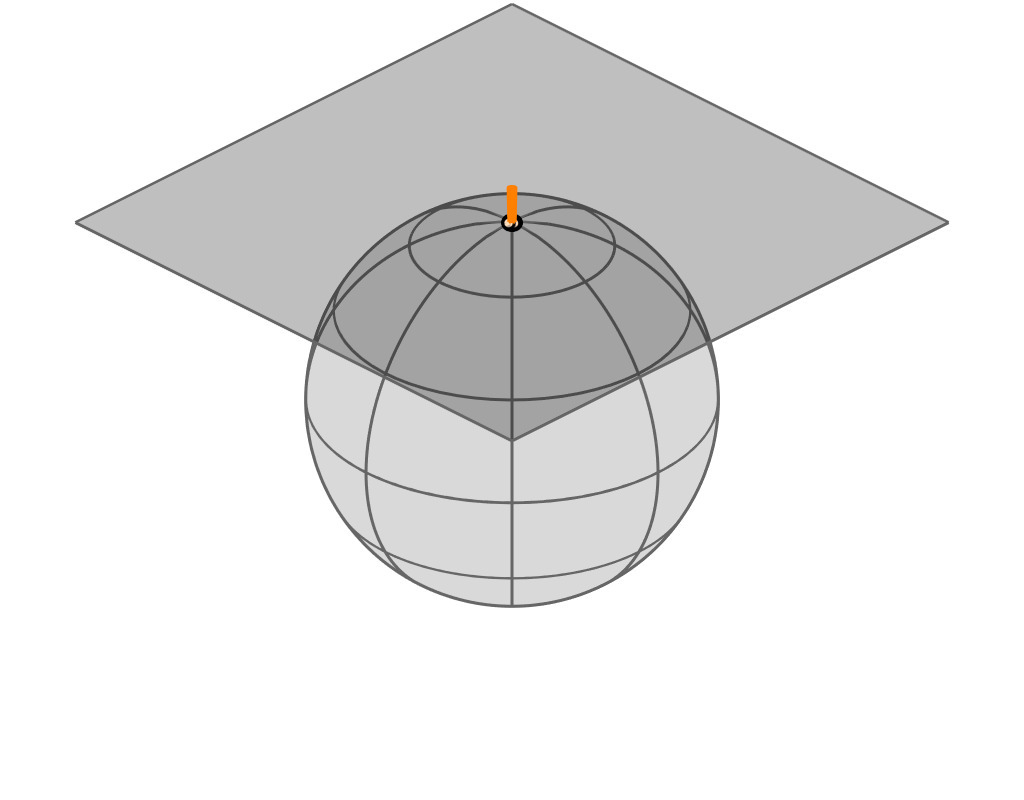
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
| A hemispherical mirror reflects parallel rays uniformly and within a spherical cap |
(see paper for mathematical proof)
Key Insight
| GGX VNDF | 🔗 | spherical caps |

|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
| A hemispherical mirror reflects parallel rays uniformly and within a spherical cap |
(see paper for mathematical proof)
Key Insight
| GGX VNDF | 🔗 | spherical caps |

|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
| A hemispherical mirror reflects parallel rays uniformly and within a spherical cap |
(see paper for mathematical proof)
Key Insight
| GGX VNDF | 🔗 | spherical caps |

|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
| A hemispherical mirror reflects parallel rays uniformly and within a spherical cap |
(see paper for mathematical proof)
Key Insight
| GGX VNDF | 🔗 | spherical caps |
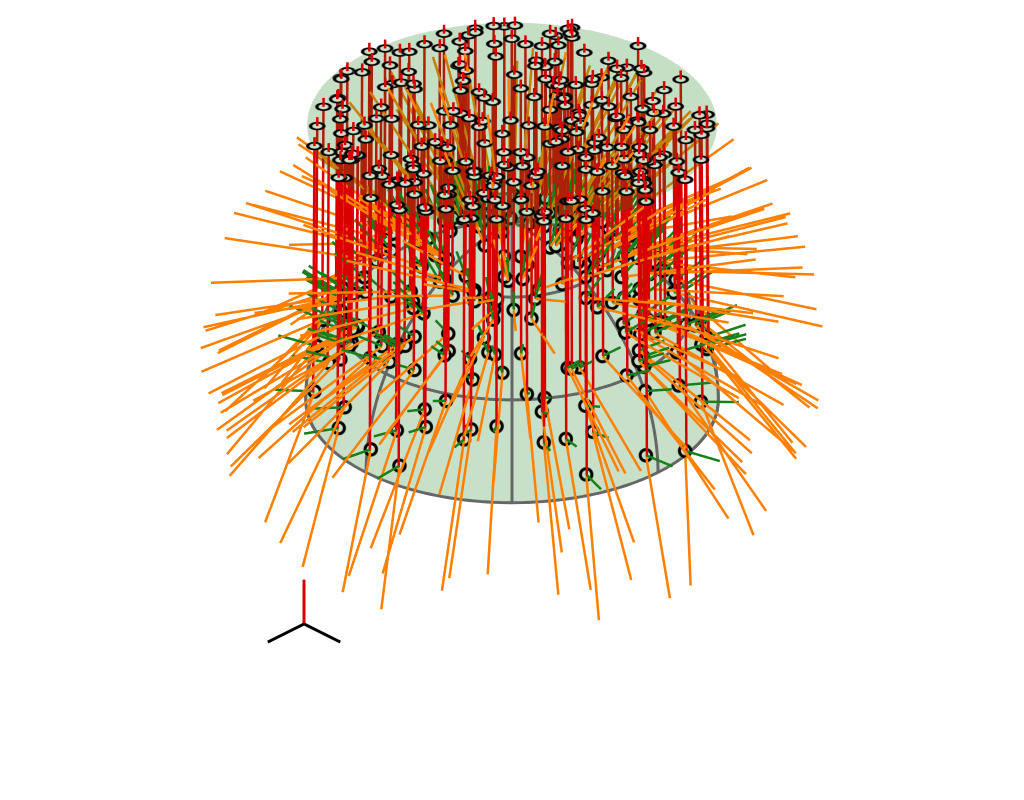
|
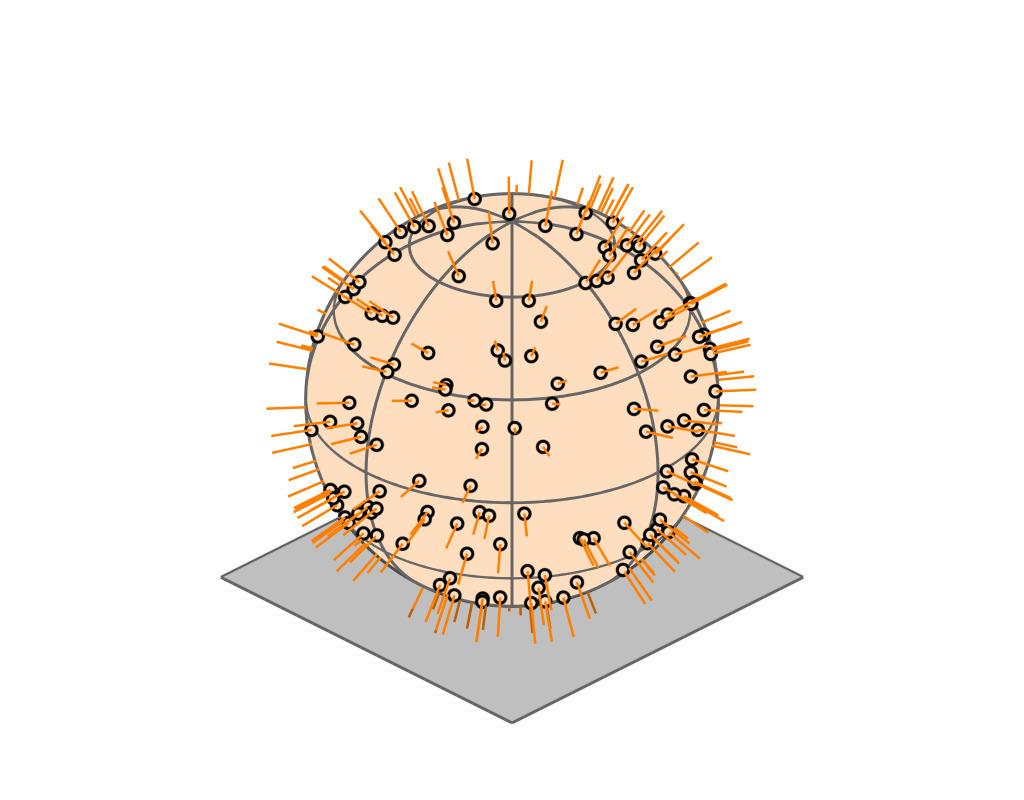
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
| A hemispherical mirror reflects parallel rays uniformly and within a spherical cap |
(see paper for mathematical proof)
Intuitions
environment:
what you see:
Intuitions
environment:
what you see:
Intuitions
environment:
what you see:
Intuitions
Key Insight
| GGX VNDF | 🔗 | spherical caps |

|
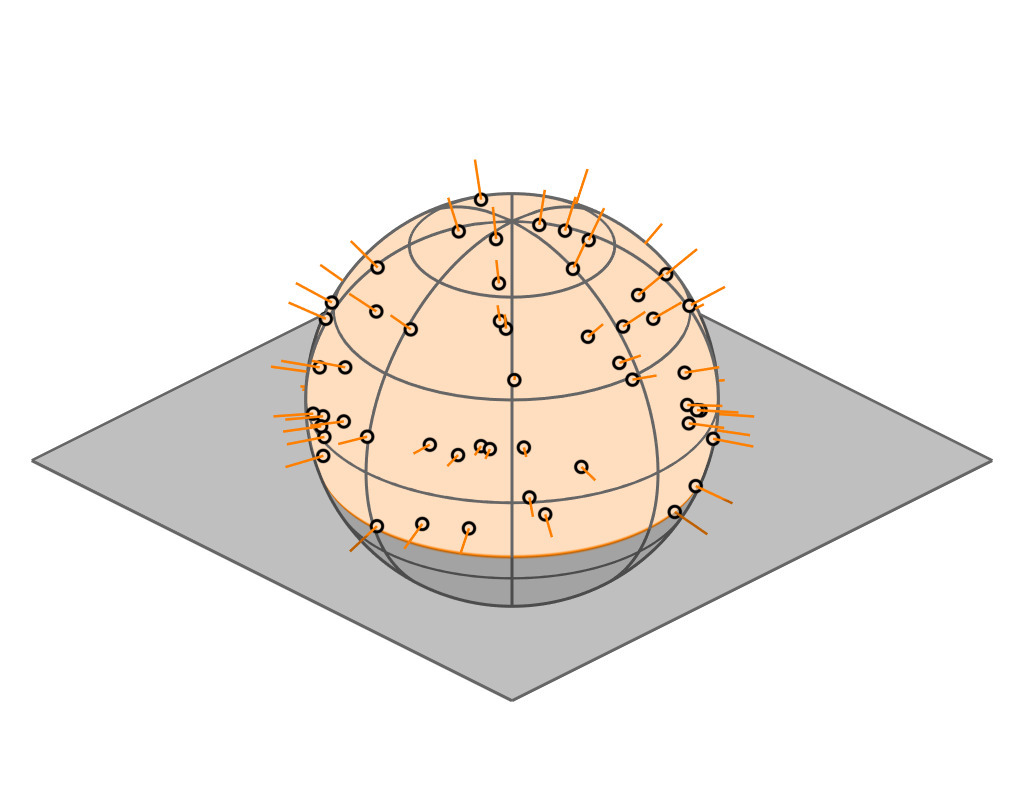
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
| A hemispherical mirror reflects parallel rays uniformly and within a spherical cap |
Our Sampling Algorithm
| GGX VNDF | 🔗 | spherical caps |

|
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
Our Sampling Algorithm
| GGX VNDF | 🔗 | spherical caps |

|
|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
$\boldsymbol{\omega}_o$
1) sample the spherical cap
Our Sampling Algorithm
| GGX VNDF | 🔗 | spherical caps |
|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
$\boldsymbol{\omega}_o$
$\boldsymbol{\omega}_o$
1) sample the spherical cap
2) compute half vector
2) compute half vector
Our Sampling Algorithm
| GGX VNDF | 🔗 | spherical caps |
|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
$\boldsymbol{\omega}_o$
$\boldsymbol{\omega}_o$
$\boldsymbol{\omega}_i$
$\boldsymbol{\omega}_o$
$+$
$\boldsymbol{\omega}_i$
$\propto$
$\boldsymbol{\omega}_m$
1) sample the spherical cap
2) compute half vector
2) compute half vector
Our Sampling Algorithm
| GGX VNDF | 🔗 | spherical caps |
|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
$\boldsymbol{\omega}_o$
$\boldsymbol{\omega}_o$
$\boldsymbol{\omega}_i$
$\boldsymbol{\omega}_o$
$+$
$\boldsymbol{\omega}_i$
$\propto$
$\boldsymbol{\omega}_m$
$\boldsymbol{\omega}_m$
1) sample the spherical cap
2) compute half vector
2) compute half vector
Our Sampling Algorithm
| GGX VNDF | 🔗 | spherical caps |
|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
$\boldsymbol{\omega}_o$
$\boldsymbol{\omega}_o$
$\boldsymbol{\omega}_i$
$\boldsymbol{\omega}_o$
$+$
$\boldsymbol{\omega}_i$
$\propto$
$\boldsymbol{\omega}_m$
$\boldsymbol{\omega}_m$
1) sample the spherical cap
2) compute half vector
2) compute half vector
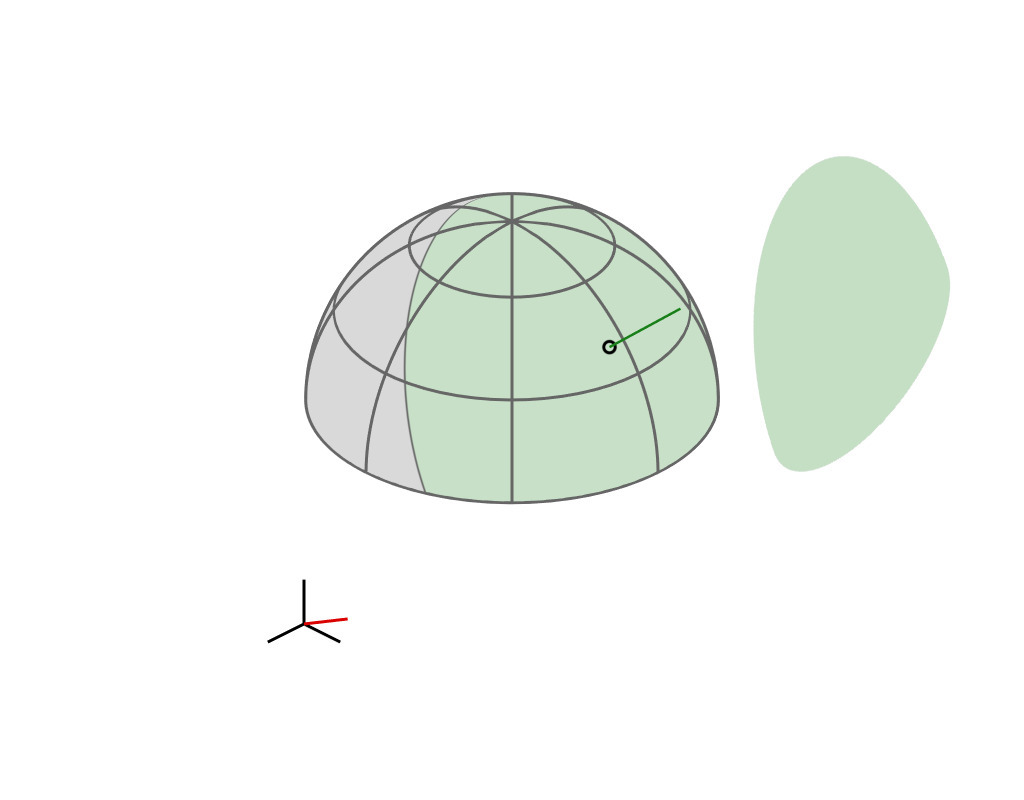
Our Sampling Algorithm
| GGX VNDF | 🔗 | spherical caps |
|

|
| incident direction |
| $\boldsymbol{\omega}_i = (x_i, \, y_i, z_i)$ |
| cutoff plane |
| $z = -$$z_i$ |
$\boldsymbol{\omega}_o$
$+$
$\boldsymbol{\omega}_i$
$\propto$
$\boldsymbol{\omega}_m$
$\boldsymbol{\omega}_o$
$\boldsymbol{\omega}_m$
1) sample the spherical cap
2) compute half vector
3) return half vector
2) compute half vector
3) return half vector
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

sample spherical cap
compute half vector
| GGX VNDF |
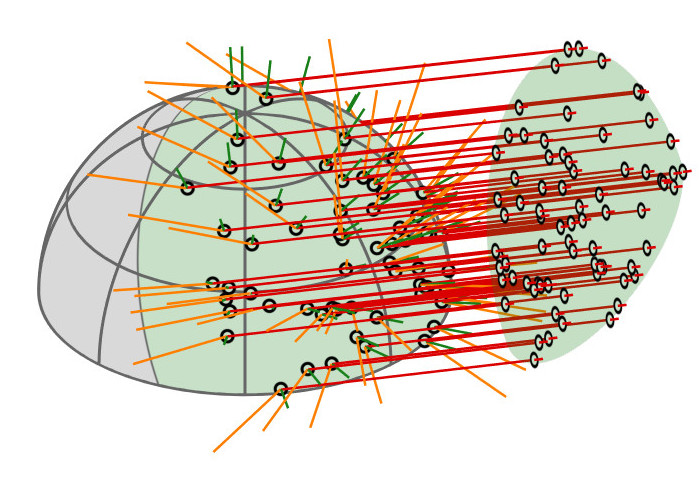
|
| spherical caps |

|
linked to
🔗
| [Heitz18] |

|
Contribution
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

sample spherical cap
compute half vector
| GGX VNDF |

|
| spherical caps |

|
linked to
🔗
| [Heitz18] |

|
build basis
sample projected area
reproject
Contribution
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

sample spherical cap
compute half vector
| GGX VNDF |

|
| spherical caps |

|
linked to
🔗
| [Heitz18] |

|
build basis
sample projected area
reproject
Contribution
Performances
| Ours |

|
|
CPU (Intel i7-13700K): 36.67% faster
|
|
GPU (Intel Arc A770): 39.25% faster
|
| [Heitz18] |

|

| [Heitz18] | ours | [Heitz18] | ours |

|

|

|

|
| 7.59% faster | 3.28% faster |
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

| GGX VNDF |

|
| spherical caps |

|
linked to
🔗
| [Heitz18] |

|
Contribution
End
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

| GGX VNDF |

|
| spherical caps |

|
linked to
🔗
Contribution
| [Heitz18] |

|

| GGX VNDF |

|
| spherical caps |

|
linked to
🔗
Contribution
| [Heitz18] |

|
| Ours |

|
|
✓ simpler
|
|
✓ faster
|
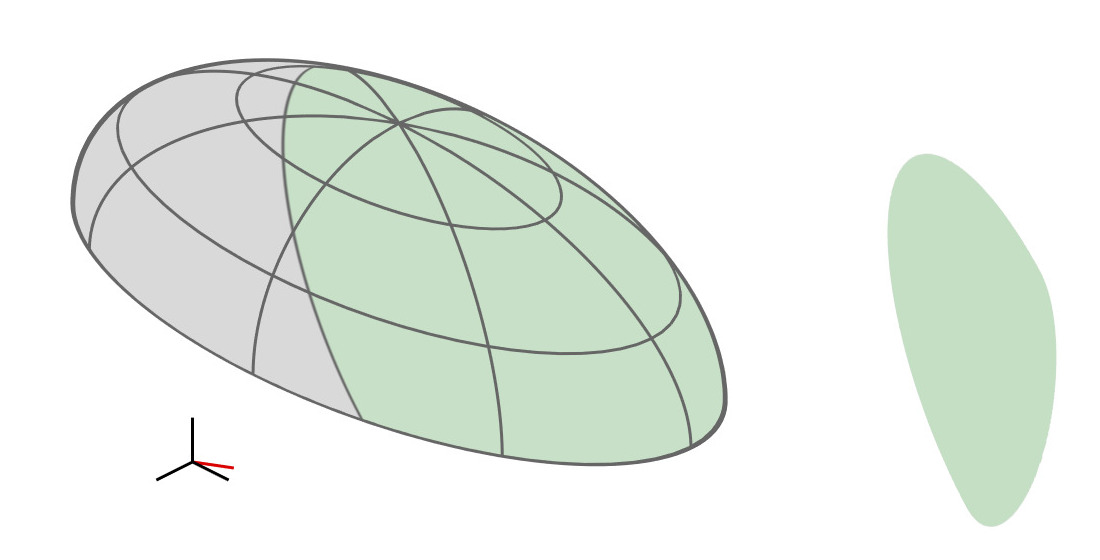
Spherical Caps

|
Spherical Caps
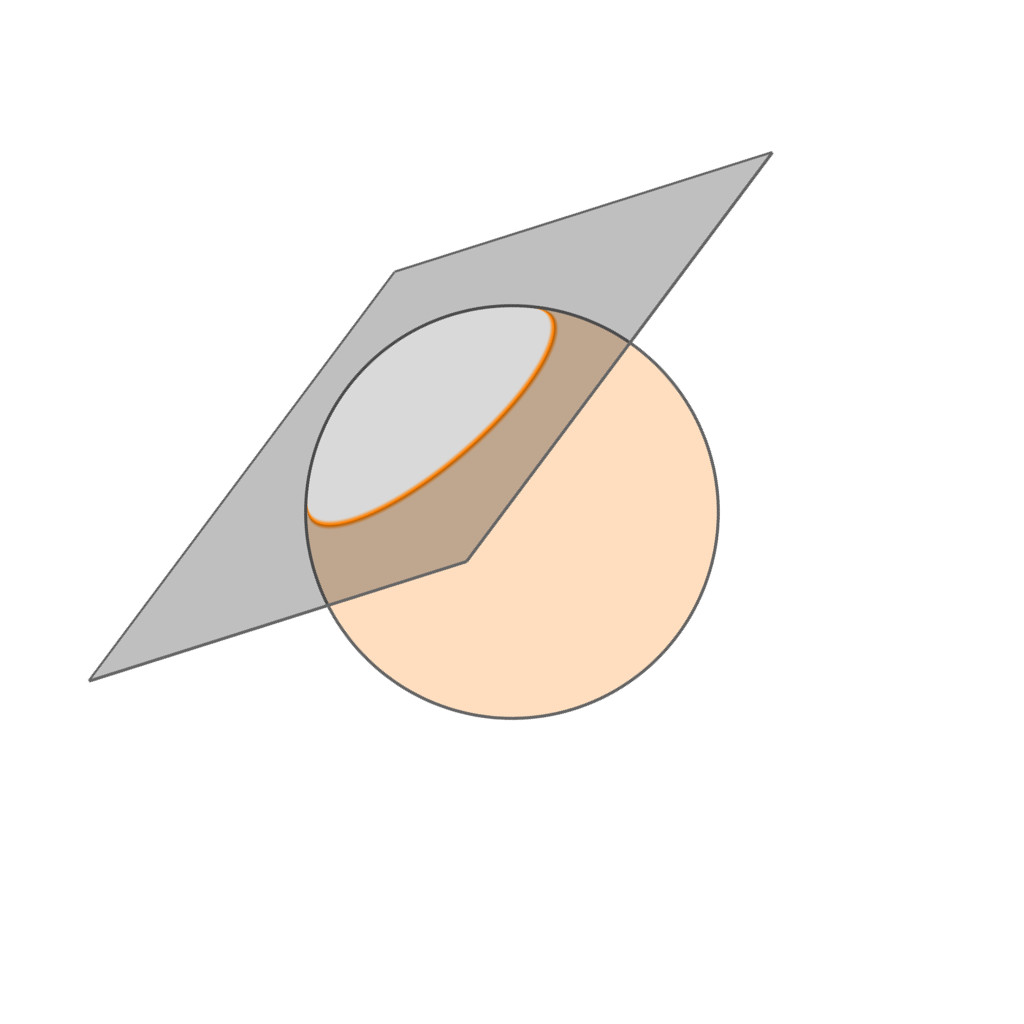
|
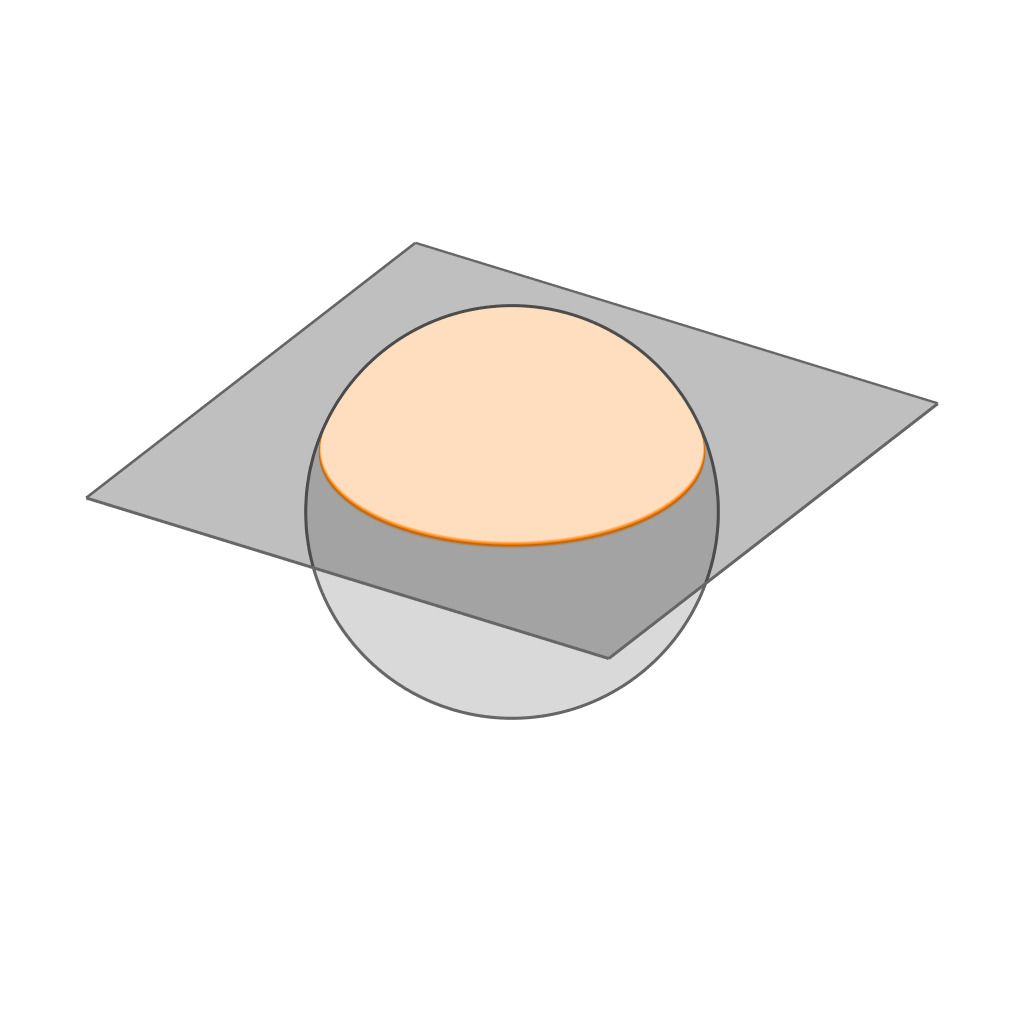
|
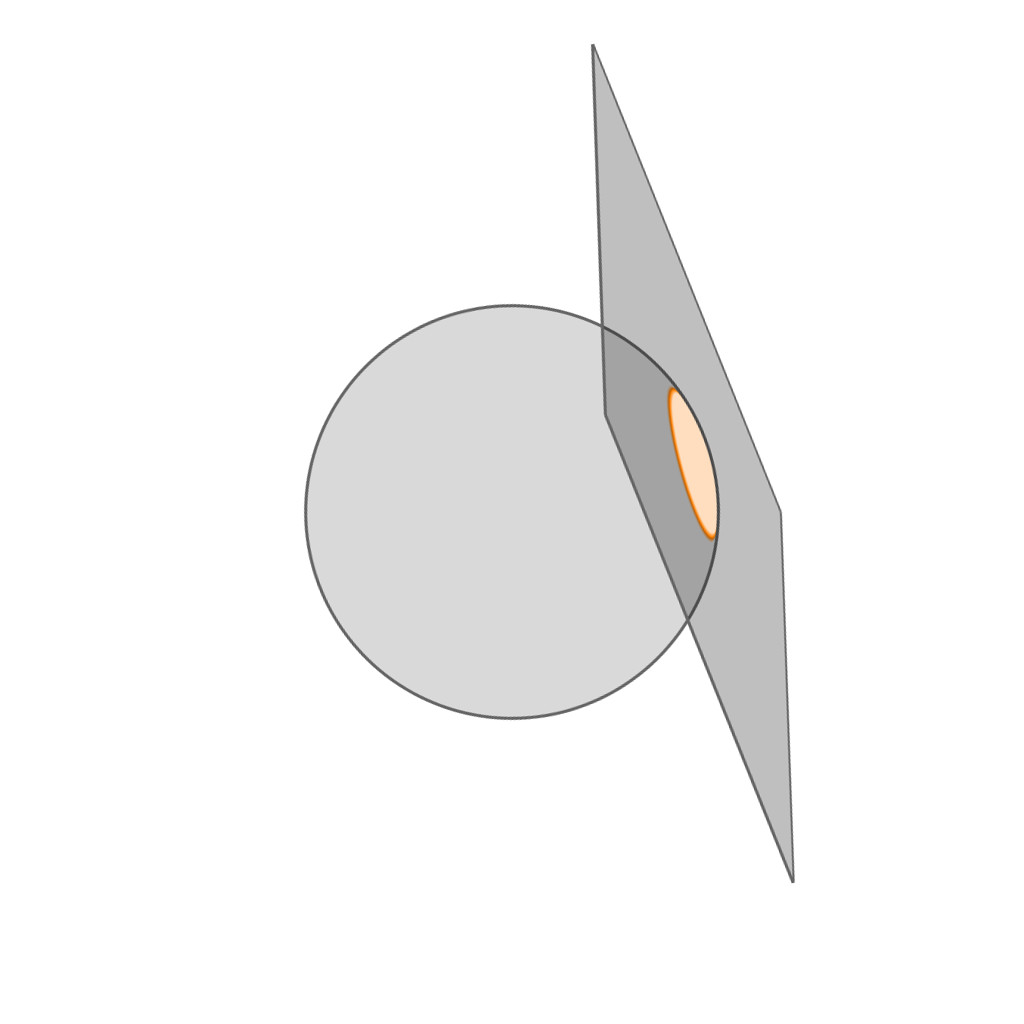
|
Spherical Caps
|

|

|
Spherical Caps

|
|

|
Spherical Caps

|

|

|
Spherical Caps

|

|

|
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

| GGX VNDF |

|
| spherical caps |

|
linked to
🔗
Contribution
| [Heitz18] |

|
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

| GGX VNDF |

|
| spherical caps |

|
linked to
🔗
| [Heitz18] |

|
Contribution
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

| GGX VNDF |
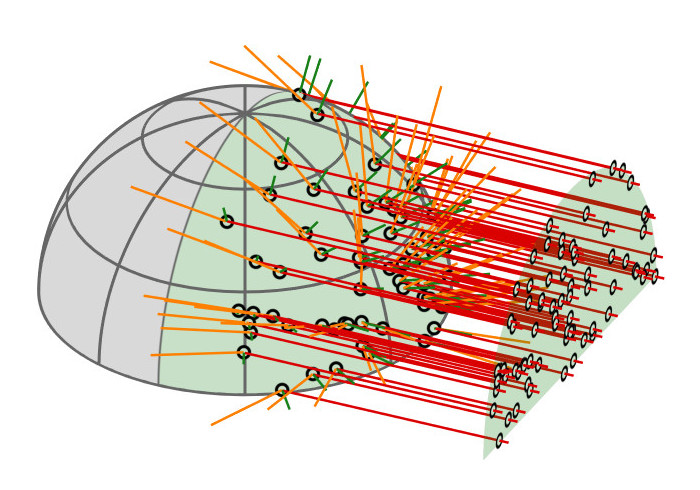
|
| spherical caps |
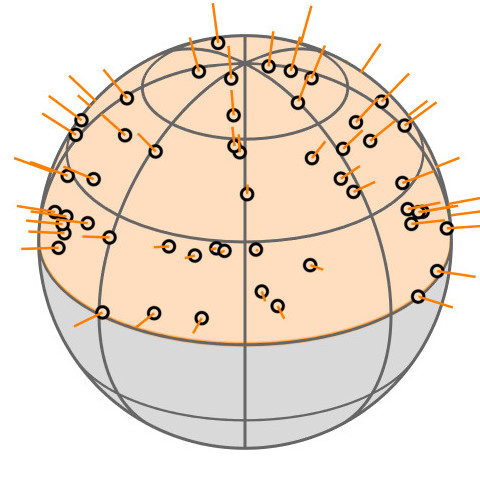
|
linked to
🔗
| [Heitz18] |

|
Contribution
| Ours |

|
|
✓ simpler
|
|
✓ faster
|

| GGX VNDF |
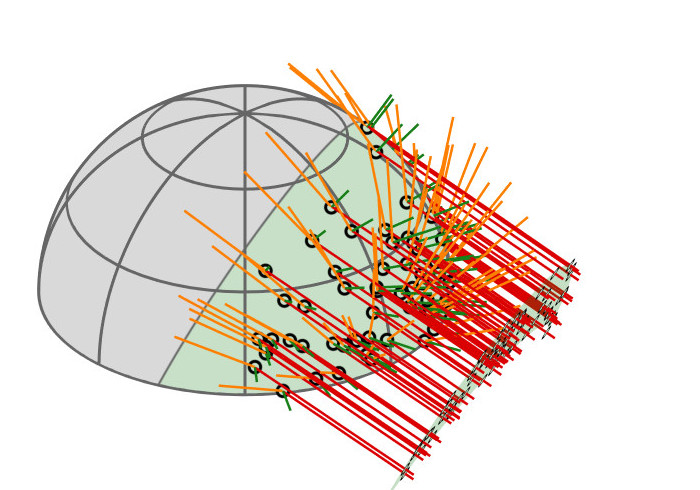
|
| spherical caps |
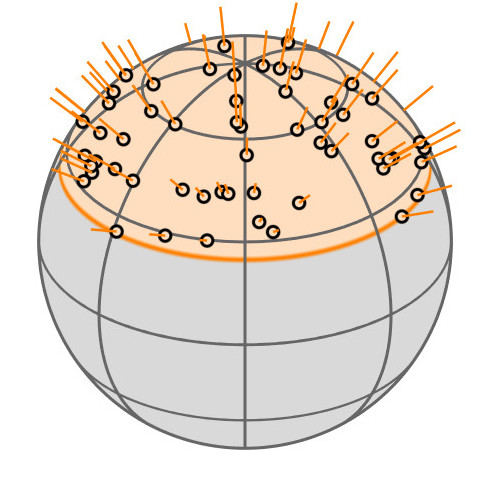
|
linked to
🔗
| [Heitz18] |

|
Contribution
Background
| [Heitz18] |

|
| GGX VNDF sampler |


VNDF

NDF

(microsurface)

(equivalent ellipsoid)
Background
| [Heitz18] |

|
| GGX VNDF sampler |


VNDF

NDF

incident direction
visible / occluded surface
(microsurface)

(equivalent ellipsoid)
visible / occluded surface
Intuitions

|

|
|